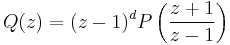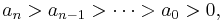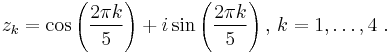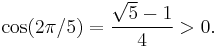Stable polynomial

A polynomial is said to be stable if either:

all its roots lie in the open left half-plane, or
all its roots lie in the open unit disk.

The first condition defines Hurwitz (or continuous-time) stability and the second one Schur (or discrete-time) stability. Stable polynomials arise in various mathematical fields, for example in control theory and differential equations. Indeed, a linear, time-invariant system (see LTI system theory) is said to be BIBO stable if and only if bounded inputs produce bounded outputs; this is equivalent to requiring that the denominator of its transfer function (which can be proven to be rational) is stable. The denominator is required to be Hurwitz stable if the system is in continuous-time and Schur stable if it is in discrete-time. Stable polynomials are sometimes called Hurwitz polynomials and Schur polynomials.

1 Properties
2 Examples
3 See also
4 External links

Properties

The Routh-Hurwitz theorem provides an algorithm for determining if a given polynomial is Hurwitz stable.
To test if a given polynomial P (of degree d) is Schur stable, it suffices to apply this theorem to the transformed polynomial

$Q(z)=(z-1)^d P\left({{z%2B1}\over{z-1}}\right)$

obtained after the Möbius transformation 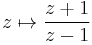$z \mapsto {{z%2B1}\over{z-1}}$ which maps the left half-plane to the open unit disc: P is Schur stable if and only if Q is Hurwitz stable.

Necessary condition: a Hurwitz stable polynomial (with real coefficients) has coefficients of the same sign (either all positive or all negative).

Sufficient condition: a polynomial 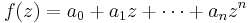$f(z)=a_0%2Ba_1 z%2B\cdots%2Ba_n z^n$ with (real) coefficients such that:

$a_n>a_{n-1}>\cdots>a_0>0,$

is Schur stable.

Product rule: Two polynomials f and g are stable (of the same type) if and only if the product fg is stable.

Examples

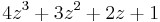$4z^3%2B3z^2%2B2z%2B1$ is Schur stable because it satisfies the sufficient condition;
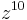$z^{10}$ is Schur stable (because all its roots equal 0) but it does not satisfy the sufficient condition;
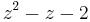$z^2-z-2$ is not Hurwitz stable (its roots are -1,2) because it violates the necessary condition;
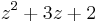$z^2%2B3z%2B2$ is Hurwitz stable (its roots are -1,-2).
The polynomial 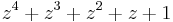$z^4%2Bz^3%2Bz^2%2Bz%2B1$ (with positive coefficients) is neither Hurwitz stable nor Schur stable. Its roots are the four primitive fifth roots of unity

$z_k=\cos\left({{2\pi k}\over 5}\right)%2Bi \sin\left({{2\pi k}\over 5}\right), \, k=1, \ldots, 4 \ .$

Note here that

$\cos({{2\pi}/5})={{\sqrt{5}-1}\over 4}>0.$

It is a "boundary case" for Schur stability because its roots lie on the unit circle. The example also shows that the necessary (positivity) conditions stated above for Hurwitz stability are not sufficient.

External links

Mathworld page

Stable polynomial

Contents

Properties

Examples

See also

External links